今天在摆弄新鲜出炉的 Sudo for Windows 时候的一个小发现
虽然截至我写下这篇博客的时候,MSDN 上 VT Sequence 的文档 还没有记载其对输出超链接的支持,但是似乎我目前的 Windows 上的 Windows Terminal 是有相应支持的。(conhost 似乎仍然只会输出普通文本)
以下是一段简短的代码展示如何使用这一功能
1 |
|
效果如下,一个可以用 Ctrl + 左键 打开的链接:
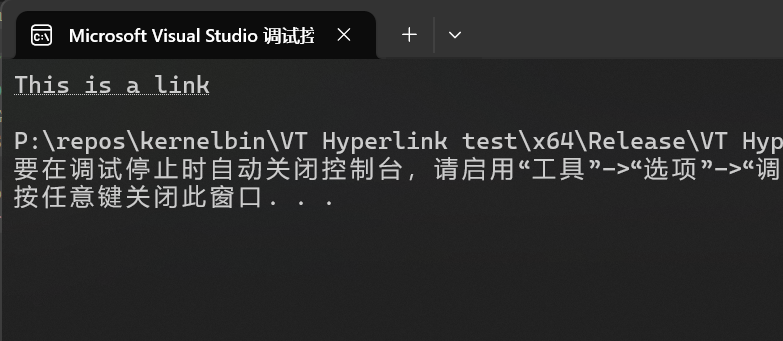
今天在摆弄新鲜出炉的 Sudo for Windows 时候的一个小发现
虽然截至我写下这篇博客的时候,MSDN 上 VT Sequence 的文档 还没有记载其对输出超链接的支持,但是似乎我目前的 Windows 上的 Windows Terminal 是有相应支持的。(conhost 似乎仍然只会输出普通文本)
以下是一段简短的代码展示如何使用这一功能
1 |
|
效果如下,一个可以用 Ctrl + 左键 打开的链接:

今天用 Chrome 的 Ctrl+S 抓了一整个网页下来想看看能不能把网页上的一个 canvas 保存下来却以失败告终。不过最后准备删掉文件的时候却有个意外的小发现
Chrome 保存下来了 foo.html 这个文件和 foo_files 这个文件夹。在我删除文件的同时,文件夹也一并消失不见了!百思不得其解的我把他们俩从垃圾桶找了出来。摆弄了一会后,发现复制时似乎这两个文件也总是被一起复制移动。我又仔细检查了文件和文件夹的属性,但一无所获。与此同时,我还在更改 foo.html 的文件名时候被提示这个文件属于 foo_files。
一番调查之后,终于发现这并非是什么神秘的 NTFS 的特殊隐藏属性,而仅仅是 explorer 干的事。对于 xxx.html 文件,explorer 会试着找到名为 xxx_files 的文件夹,并且一并操作这两个文件。这个行为阿硬记录在了[这里],名为 Connected Files
SAL 中 _Out_writes_ 和 _Out_writes_all_ 的区别
经常写 Windows 程序的人一定不会对 SAL 陌生。SAL(Source Annotation Language)可以帮助你在编译的时候就检测出一些可能的运行时错误,比如数组越界。不是很了解? >阿硬文档传送门<
之前一直没有留意有些参数的 Annotation 后附带的 _all_ 的含义,比如 _Out_writes_all_(s)。什么时候该用这个,什么时候又该用不带 _all_ 的 _Out_writes_(s) 呢?
_Out_writes_(s) 表示传入数组可以写入的有效长度是 s,并且这个函数会往这个参数内写入一些东西,但是现在并不知道具体会写入多长的数据。比如 strcpy 就适用这种情况:虽然肯定知道 dest 会被从 src 中复制过来一段数据,但是多长…起码这个长度没有一个现成的变量可以指明。以下是阿硬文档中的栗子🌰:
1 | typedef _Null_terminated_ wchar_t *PWSTR; |
_Out_writes_all_(s) 则说明除了数组可以写入的有效长度是 s,也保证调用后整个数组都是有效的,这实际上等效于写 _Out_writes_to_(s, s)。适用的情况有 memset,因为 memset 一定会把整个数组全部填充满。以下是 memset 在 MSVC 里的声明:
1 | void* __cdecl memset( |
个人认为 SAL 还是相当强大好用的,苦于文档太少只能自己摸索使用姿势和 best practise,(当然上述内容还是有在文档记录的…)希望阿硬赶紧能把 SAL 的文档写完善一些((
本来以为算法竞赛退役之后,可能没什么机会再碰数论相关内容了。没想到这么快数论就又找上我了(笑)这篇文章是我自己对 Curve25519 的学习和理解。俺数学功底薄弱,非常菜菜🥬,如有疏漏请指出!非常感谢数学迷和其他朋友在数学方面给我的指导
Curve25519 是一个基于椭圆曲线的 Diffie-Hellman(DH) 函数。基于椭圆曲线的密码学是当下最为安全和先进的公私钥加密系统。
通常椭圆曲线加密算法需要对公钥进行验证,以防止小子群攻击和无效曲线攻击。但是 Curve25519 却不需要对公钥进行验证。在 cr.yp.to 上有如下记录:
How do I validate Curve25519 public keys?
Don’t. The Curve25519 function was carefully designed to allow all 32-byte strings as Diffie-Hellman public keys.
这是为什么呢?
TL;DR 对公钥进行验证的原因是对应的点可能并没有落在椭圆曲线上,而是落在曲线的二次扭曲上。如果二次扭曲是不安全的,会使计算出的共享密钥“有问题”从而泄露信息。而 Curve25519 曲线的参数经过精心挑选,对应的二次扭曲也是安全的。
看不懂?打个比方吧。 你是奇异博士,你挑选了一块你战无不胜的空间领域,但是并在其他空间领域里都是如此。每个空间都附带一个镜像空间 (也就是二次扭曲),虽然你在本体空间战无不胜,但镜像空间内并不一定。本来你要费力辨别狡猾的邪恶魔法师是否是在镜像空间内向你发起挑战的,如果是那么你要拒绝挑战 (检查公钥)。后来你找到了一个空间,在这个空间和这个空间的镜像空间里你都百战百胜。于是便可不费力辨别邪恶魔法师是在哪向你发出挑战的了 (Curve25519 的设计)。
还看不懂?那要不直接看数学原理?
在开始之前,不妨先简单介绍一下椭圆曲线算法大概是如何进行的:
椭圆曲线算法会事先选择一个素数 $q$,把所有运算转换为在 $[0, q-1]$ 内的模 $q$ 整数运算。事先规定一条椭圆曲线和这条曲线上的一个点 $G$ 作为基点。算法会选择一个随机整数 $k$ 作为私钥;并计算值 $P=k*G$ 作为公钥,之后便是使用 $DH$ 函数根据自己的私钥和对方的公钥计算出共享密钥了。至于如何定义两个点的加法和使用快速幂的思想计算点的标量乘法的这里就不过多赘述了,相关的介绍应该有很多了。
在一条曲线上如果对一个点重复的加自身,最终会兜回这个点自身形成一个循环。这个循环的长度再减一叫做这个点的阶。
椭圆曲线在设计的时候都会确保基点 $G$ 的阶有一个足够大的素因子的原因是为了防止小子群攻击。如果 $G$ 的阶可以被分解为好多个小素数的乘积,那主动攻击者可以利用这个性质缩小共享密钥可能的取值范围,并且暴力尝试所有可能的共享密钥之后得出对方私钥的一部分信息,然后在多次探测后使用中国剩余定理求解出私钥。这种情况同样可能会发生在攻击者发送了一个没有落在规定曲线上的“假”公钥而没有对公钥进行验证的情况下。
对于 Curve25519 这类采用 $P$ 点的横坐标 $x$ 作为公钥的协议来说,要验证公钥是否有效就需要验证椭圆曲线 $y^2 = x^3 + Ax^2 + Bx + C\pmod{q}$ 是否有解。$x$ 是已知的,所以方程右侧的值是固定的,那么判断是否有解其实就是判断是否存在一个 $y$ 使得 $y^2$ 的值在取模意义下等于方程右侧的值 ———— 二次剩余。
椭圆曲线等式右侧的值 $f(x) = x^3 + Ax^2 + Bx + C$ 算出来要么是一个二次剩余,要么不是二次剩余/*废话*/,也就是二次非剩余。
由于两个二次非剩余相除可以得到一个二次剩余,所以虽然在右侧是二次非剩余的情况下点并不落在椭圆曲线上,但是方程 $y^2 = (x^3 + Ax^2 + Bx + C) / d$ 却会有解,其中 $d$ 是模 $q$ 意义下的一个二次非剩余。把 $d$ 乘在等式左侧可以得到:$dy^2 = x^3 + Ax^2 + Bx + C$。
一通操作之后会发现这个方程可以写为 $y^2 = x^3 + dAx^2 + d^2Bx + d^3C$,也符合椭圆曲线的形式。
证明方法应该有很多,比如使用欧拉准则:
$d$ 是模 $p$ 的二次剩余当且仅当:
$d^{\frac{p-1}{2}} \equiv 1 \pmod{p}$
$d$ 是模 $p$ 的非二次剩余当且仅当:
$d^{\frac{p-1}{2}} \equiv -1 \pmod{p}$
不难推出两个二次非剩余相除可以得到一个二次剩余
将方程左右两侧同时乘以 $d^3$,得到:$d^4y^2 = d^3x^3 + d^3Ax^2 + d^3Bx + d^3C$
进行换元:$y’ = d^2y, x’=dx$,得到:$y’^2 = x’^3 + dAx’^2 + d^3Bx’ + d^3C$
令 $y = y’, x = x’$,得到:$y^2 = x^3 + dAx^2 + d^2Bx + d^3C$
举一个实际的栗子🌰,比如我们有一条椭圆曲线 $y^2 = x^3 + 3x^2 +2\pmod{7}$,在模 $7$ 意义下 $1, 4, 2$ (分别是 $1^2\pmod{7}, 2^2\pmod{7}, 3^2\pmod{7}$)是二次剩余,剩下的 $3, 5, 6$ 是二次非剩余。
我们可以随意选取一个二次非剩余(假设是 $5$)乘在等式左侧,就可以得到一条椭圆曲线的二次扭曲:
$5y^2 = x^3 + 3x^2 +2\pmod{7}$
选取不同的二次剩余 $d$ 得到的式子经过一个简单的换元就一样了,见解答
如果公钥对应的点落在了椭圆曲线之外,那么这个公钥实际上对应着来自二次扭曲上的一个点。而二次扭曲如果是不安全的,(也就是阶可以被分解为多个小素数)就使得攻击者仍然可以进行前面提到过的小子群攻击了。
如果…二次扭曲也是安全的呢?
Curve25519 正是这么设计的。Curve25519 曲线本身和 Curve25519 所对应的二次扭曲都是安全的,哪怕攻击者使用了一个落在曲线外的 $x$ 坐标作为公钥,这个点也是落在同样保证安全的二次扭曲上的,攻击者仍然没有办法缩小计算出的共享密钥的范围。
具体而言 Curve25519 曲线本身上的点数是 $8 * p1$,其中 $p1$ 是素数 $2^{252} + 27742317777372353535851937790883648493$
Curve25519 曲线的二次扭曲上的点数是 $4 * p2$,其中 $p2$ 是素数 $2^{253} - 55484635554744707071703875581767296995$
这里没有选取点数本身是素数的曲线,原因是 Curve25519 使用的是形式为蒙哥马利的椭圆曲线,这类椭圆曲线更易于计算,但是这类曲线阶数只能是 $4$ 的倍数。
这也是 Curve25519 在进行生成私钥的时候抹除了最低三位的原因
这正是 Curve25519 在 Diff-Hellman 中不需要验证公钥的原因。有关 Curve25519 在设计时的更多考量,可以翻阅 Curve25519 的论文
最近在读 Wireguard-NT 的源代码中 SIMD 优化部分时,发现在几乎每个函数的入口处都有如下汇编代码:
1 | SomeFunction PROC PUBLIC |
对此感到非常奇怪。在一番调查后,发现这段数据对应的是 ENDBR64 指令,属于英特尔控制流强制技术(CET)的一部分。
CET 技术主要由影子堆栈 (Shadow Stack, SS) 和间接分支跟踪 (Indirect Branch Tracking, IBT) 组成,而这里的 ENDBR64 指令就属于后者,这些技术都是为了一定程度防止攻击者通过篡改跳转类型指令的目的地址构造攻击。ENDBR64 是 64 位下的,自然也有对应的 32 位版本。
在启用 IBT 的情况下,间接跳转和调用类型的指令不能跳转到任意的地址,如果跳转到的目标地址没有对应的 ENDBR 指令则会触发异常,相当于是规定了只能跳转到指定的标记有 ENDBR 指令的地址。在较老的不支持的机器上,这条指令会被视为 NOP。
gcc 可以通过参数 -fcf-protection=branch 来自动生成相关代码,但似乎我编写这篇博客的时候 MSVC 还没有相应的支持
SS 技术则是通过把返回地址在另一个独立的堆栈里再存储一份返回地址,并在返回时对一式两份的地址进行比较来增加构造攻击的难度。(不过这类技术似乎会影响 setjmp 和 longjmp 函数的兼容性,可能需要额外做一些工作)
很久以来一直想有空写个自己的博客,大概从高一时就有这个想法了。却不知为何迟迟没有行动,时至今日才建起了自己的博客。
本来想在博客上写一些算法笔记和一些技术文章,不过如今已经从 OI/ACM 退役,可能会分享更多技术和生活文章吧。
可能博客更新频率并不会很高,打算偶尔学到有趣的内容再分享,也希望这个博客能促进我有动力学点新东西吧